How to: Unification
Note: This is a work in progress. When it is complete these notes will be removed.
Note: Do not reply to this topic, questions, concerns, comments, etc. are to handled in
Wiki Discussion: How to - Unification
Note: This is just to get the topic started and hopefully others to jump in and make this useful. Even if you are brand new to Prolog, this is such a basic and fundamental concept that you can and should join in to help improve the value of this Wiki. Join the discussion at Wiki Discussion: How to - Unification
Note: This is a wiki and if you have Trust level: Basic you can edit this by clicking on the pencil icon in the lower right.
These topics also have history so they can be rolled-back if needed.
While there are ways of unifying, e.g. e-unification, this is only going to talk about syntactic unification as used in Prolog.
For unification of syntax there is basically only three things to be aware of
- Values
- Variables
- Structures that have a name as a value and are made up of values, variables and structures.
A value is a constant that will not change.
A variable can change but only once, hence the words unbound and bound as opposed to assigned.
A structure will have name called a functor and one or more arguments. While some things may not seem like structures such as list, [a,b,c] they really are in concept. See write_canonical/1
Unification Examples
Based on Wikipedia
| Symbols | |
|---|---|
| Variables | Constants |
| In Prolog: Start with upper case letter | In Prolog: Start with lower case letter |
| X Y Z | a b f g |
| Δ Φ Ω | π λ ε |
| ⌂ ⌀ ⌘ | ☃ ⍟ ∎ |
| Rectangles | Ovals |
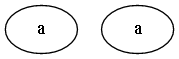
| a = a | π = π | ☃ = ☃ |
|
Unify: true MGU: {} |
Unify: true MGU: {} |
Unify: true MGU: {} |
|
SWI-Prolog: ?- =(a,a). true. |
SWI-Prolog: ?- =(π,π). true. |
SWI-Prolog: ?- =(☃,☃). true. |


| a = b | π = λ | ☃ = ⍟ |
| Unify: false | Unify: false | Unify: false |
|
SWI-Prolog: ?- =(a,b). false. |
SWI-Prolog: ?- =(π,λ). false. |
SWI-Prolog: ?- =(☃,⍟). false. |



| X = X | Δ = Δ | ⌂ = ⌂ |
|
Unify: true MGU: {} |
Unify: true MGU: {} |
Unify: true MGU: {} |
|
SWI-Prolog: ?- =(X,X). true. |
SWI-Prolog: ?- =(Δ,Δ). true. |
SWI-Prolog: ?- =(⌂,⌂). true. |



| a = X | π = Δ | ☃ = ⌂ |
|
Unify: true MGU: { X ↦ a } |
Unify: true MGU: { Δ ↦ π } |
Unify: true MGU: { ⌂ ↦ ☃ } |
|
SWI-Prolog: ?- =(a,X). X = a. |
SWI-Prolog: ?- =(π,Δ). Δ = π. |
SWI-Prolog: ?- =(☃,⌂). ⌂ = ☃. |



| X = Y | Δ = Φ | ⌂ = ⌀ |
|
Unify: true MGU: { X ↦ Y } |
Unify: true MGU: { Δ ↦ Φ } |
Unify: true MGU: { ⌂ ↦ ⌀ } |
|
SWI-Prolog: ?- =(X,Y). X = Y. |
SWI-Prolog: ?- =(Δ,Φ). Δ = Φ. |
SWI-Prolog: ?- =(⌂,⌀). ⌂ = ⌀. |



| f(a,X) = f(a,b) | λ(π,Φ) = λ(π,ε) | ⍟(☃,⌀) = ⍟(☃,∎) |
|
Unify: true MGU: { X ↦ b } |
Unify: true MGU: { Φ ↦ ε } |
Unify: true MGU: { ⌀ ↦ ∎ } |
|
SWI-Prolog: ?- =(f(a,X),f(a,b)). X = b. |
SWI-Prolog: ?- =(λ(π,Φ),λ(π,ε)). Φ = ε. |
SWI-Prolog: ?- =(⍟(☃,⌀),⍟(☃,∎)). ⌀ = ∎. |



| f(a) = g(a) | ε(λ) = π(λ) | ∎(⍟) = ☃(⍟) |
| Unify: false | Unify: false | Unify: false |
|
SWI-Prolog: ?- =(f(a),g(a)). false. |
SWI-Prolog: ?- =(ε(λ),π(λ)). false. |
SWI-Prolog: ?- =(∎(⍟),☃(⍟)). false. |



| f(X) = f(Y) | π(Ω) = π(Δ) | ☃(⌘) = ☃(⌂) |
|
Unify: true MGU: { X ↦ Y } |
Unify: true MGU: { Ω ↦ Δ } |
Unify: true MGU: { ⌘ ↦ ⌂ } |
|
SWI-Prolog: ?- =(f(X),f(Y)). X = Y. |
SWI-Prolog: ?- =(π(Ω),π(Δ)). Ω = Δ. |
SWI-Prolog: ?- =(☃(⌘),☃(⌂)). ⌘ = ⌂. |



| f(X) = g(Y) | ε(Ω) = π(Φ) | ∎(⌘) = ☃(⌀) |
| Unify: false | Unify: false | Unify: false |
|
SWI-Prolog: ?- =(f(X),g(Y)). false. |
SWI-Prolog: ?- =(ε(Ω),π(Φ)). false. |
SWI-Prolog: ?- =(∎(⌘),☃(⌀)). false. |



| f(X) = f(Y,Z) | λ(Ω) = λ(Φ,Δ) | ⍟(⌘) = ⍟(⌀,⌂) |
| Unify: false | Unify: false | Unify: false |
|
SWI-Prolog: ?- =(f(X),f(Y,Z)). false. |
SWI-Prolog: ?- =(λ(Ω),λ(Φ,Δ)). false. |
SWI-Prolog: ?- =(⍟(⌘),⍟(⌀,⌂)). false. |



| f(g(X)) = f(Y) | π(λ(Φ)) = π(Δ) | ☃(⍟(⌀)) = ☃(⌂) |
|
Unify: true MGU: { Y ↦ g(X) } |
Unify: true MGU: { Δ ↦ λ(Φ) } |
Unify: true MGU: { ⌂ ↦ ⍟(⌀) } |
|
SWI-Prolog: ?- =(f(g(X)),f(Y)). Y = g(X). |
SWI-Prolog: ?- =(π(λ(Φ)),π(Δ)). Δ = λ(Φ). |
SWI-Prolog: ?- =(☃(⍟(⌀)),☃(⌂)). ⌂ = ⍟(⌀). |



| f(g(X),X) = f(Y,a) | ε(λ(Φ),Φ) = ε(Δ,π) | ∎(⍟(⌀),⌀) = ∎(⌂,☃) |
|
Unify: true MGU: { X ↦ a, Y ↦ g(a) } |
Unify: true MGU: { Φ ↦ π, Δ ↦ λ(π) } |
Unify: true MGU: { ⌀ ↦ ☃, ⌂ ↦ ⍟(☃) } |
|
SWI-Prolog: ?- =(f(g(X),X),f(Y,a)). X = a, Y = g(a). |
SWI-Prolog: ?- =(ε(λ(Φ),Φ),ε(Δ,π)). Φ = π, Δ = λ(π). |
SWI-Prolog: ?- =(∎(⍟(⌀),⌀),∎(⌂,☃)). ⌀ = ☃, ⌂ = ⍟(☃). |



| X = f(X) | Φ = π(Φ) | ⌀ = ☃(⌀) |
|
Unify: false Occurs check: fails |
Unify: false Occurs check: fails |
Unify: false Occurs check: fails |
|
SWI-Prolog: ?- =(X,f(X)). X = f(X). |
SWI-Prolog: ?- =(Φ,π(Φ)). Φ = π(Φ). |
SWI-Prolog: ?- =(⌀,☃(⌀)). ⌀ = ☃(⌀). |
|
SWI-Prolog: ?- unify_with_occurs_check(X,f(Y,X)) false. |
SWI-Prolog: ?- unify_with_occurs_check(Φ,π(Φ)). false. |
SWI-Prolog: ?- unify_with_occurs_check(⌀,☃(⌀)). false. |



|
X = Y, Y = a |
Ω = Δ, Δ = ε |
⌘ = ⌂, ⌂ = ∎ |
|
Unify: true MGU: { Y ↦ a, X ↦ a } |
Unify: true MGU: { Δ ↦ ε, Ω ↦ ε } |
Unify: true MGU: { ⌂ ↦ ∎, ⌘ ↦ ∎ } |
|
SWI-Prolog: ?- X=Y,Y=a. X = Y, Y = a. or ?- =(X,Y),=(Y,a). X = Y, Y = a. |
SWI-Prolog: ?- Ω=Δ,Δ=ε. Ω = Δ, Δ = ε. or ?- =(Ω,Δ),=(Δ,ε). Ω = Δ, Δ = ε. |
SWI-Prolog: ?- ⌘=⌂,⌂=∎. ⌘ = ⌂, ⌂ = ∎. or ?- =(⌘,⌂),=(⌂,∎). ⌘ = ⌂, ⌂ = ∎. |



| a = Y, X = Y |
λ = Φ, Δ = Φ |
⍟ = ⌀, ⌂ = ⌀ |
|
Unify: true MGU: { Y ↦ a, X ↦ a } |
Unify: true MGU: { Φ ↦ λ, Δ ↦ λ } |
Unify: true MGU: { ⌀ ↦ ⍟, ⌂ ↦ ⍟ } |
|
SWI-Prolog: ?- a=Y,X=Y. Y = X, X = a. or ?- =(a,Y),=(X,Y). Y = X, X = a. |
SWI-Prolog: ?- λ=Φ,Δ=Φ. Φ = Δ, Δ = λ. or ?- =(λ,Φ),=(Δ,Φ). Φ = Δ, Δ = λ. |
SWI-Prolog: ?- ⍟=⌀,⌂=⌀. ⌀ = ⌂, ⌂ = ⍟. or ?- =(⍟,⌀),=(⌂,⌀). ⌀ = ⌂, ⌂ = ⍟. |



| X = a, b = X |
Δ = λ, ε = Δ |
⌂ = ⍟, ∎ = ⌂ |
| Unify: false | Unify: false | Unify: false |
|
SWI-Prolog: ?- X=a,b=X. false. or ?- =(X,a),=(b,X). false. |
SWI-Prolog: ?- Δ=λ,ε=Δ. false. or ?- =(Δ,λ),=(ε,Δ). false. |
SWI-Prolog: ?- ⌂=⍟,∎=⌂. false. or ?- =(⌂,⍟),=(∎,⌂). false. |



For a visual representation that shows the unification/substitutions durning the executation of simple Prolog programs see: Prolog Visualizer